ЗАДАНИЯ ОЛИМПИАДЫ
Задачи теоретической части
В предложенных задачах требуется дать словесное описание алгоритма решения предложенной задачи (если не оговаривается что-то другое). При проверке решений (алгоритмов) будут учитываться следующие параметры:
а) четкость описания алгоритма,
б) результативность (алгоритм в любом случае должен давать некоторый результат),
в) корректность (алгоритм должен давать правильный ответ при любых корректных входных данных),
г) оптимальность (следует привести по возможности наиболее оптимальный по количеству шагов алгоритм; из нескольких корректных алгоритмов больше баллов получит наиболее оптимальный).
Решения задач теоретической части оформляются в виде документа Microsoft Word в соответствии с техническими требованиями и загружаются для проверки в Виртуальном кабинете.
1. Конверты
По краю очень большого круглого стола с равными интервалами разложены небольшие конверты, в каждом из которых лежат деньги. Известны суммы, лежащие в каждом конверте. Опишите алгоритм, позволяющий провести прямую через центр стола, разделяющую конверты на два множества с одинаковой суммой денег. Прямая не должна проходить по конвертам. Если такой прямой нет – сообщите об этом.
2. Алгоритм
Функция S, аргументами которой являются два действительных числа, задана следующей блок-схемой:
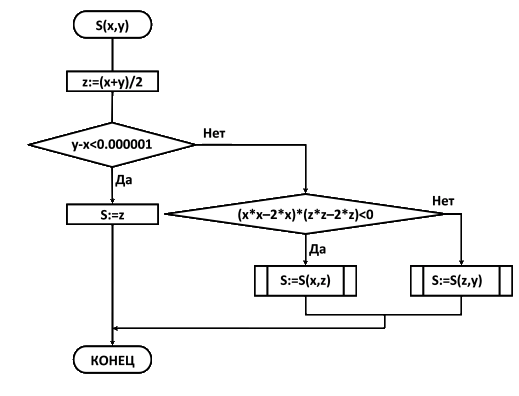
Какое значение примет переменная w после выполнения следующих команд:
а) w := S(3, 4);
б) w := S(1, 4)?
3. Преобразования числа
С написанным на доске числом производят следующее действие. Каждую его цифру возводят в квадрат, все результаты суммируют и результат выписывают на доску вместо исходного числа. Так продолжается сколько угодно раз. Опишите алгоритм, определяющий, можно ли таким образом получить из начального натурального числа N заданное натуральное число M? Обоснуйте конечность разработанного алгоритма.
4. Найдите карточку
На столе в виде прямоугольника N×M лежат карточки, на которых написаны числа. Карточки лежат числами вниз. Известно, что в каждой строке числа упорядочены по возрастанию слева направо и в каждом столбце числа упорядочены по возрастанию сверху вниз. Задаётся число X. За возможно меньшее количество переворачиваний карточек требуется найти карточку с числом X или заявить, что такой карточки на столе нет.
Решите задачу в двух случаях:
а) N=10, M=10;
б) N=4, M=17.
5. Двоичные числа по кругу
Заданы натуральные N и K. Требуется расположить по кругу все N-разрядные двоичные числа, в записи которых содержится ровно K единиц, чтобы соседние числа различались только в двух разрядах. Ведущие разряды двоичного числа могут быть нулевыми.
Например при N=4 и K=2 числа можно расположить так:
1100
1010
1001
0101
0011
0110
Опишите алгоритм, как это можно сделать при произвольных N и K.
Задачи практической части
В практической части олимпиады требуется написать решения задач – программы, соответствующие техническим требованиям и выполняющие оговоренные условиями задачи действия, на языке Паскаль или Си.
Для проверки принимаются только исходные тексты программ (файлы *.pas, *.c, *.cpp) в соответствии с техническими требованиями. Программы (исходные тексты) загружаются для проверки в Виртуальном кабинете, сразу компилируются и проверяются на наборе тестов, после чего участнику выдается результат. Допускается вносить изменения в программы произвольное количество раз и загружать программы для повторной проверки.
Внимание: загрузка работ будет возможна с 20 ноября (c 15:00 МСК). Загружается только исходный текст программы (файл *.pas, *.c, *.cpp) без архивирования.
С учетом того, что проверка работ практической части ведется а автоматическом режиме, следует внимательно следить за форматами выходных файлов: несоответствие формата выходного файла может привести к тому, что результат прохождения теста не будет засчитан.
Входные данные берутся из текстового файла input.txt, результат выполнения программы выводится в файл output.txt в установленном формате. Программа ничего не должна запрашивать для ввода с клавиатуры и не должна ничего выводить на экран.
Ограничения на время выполнения программы по каждому из тестов: 10 секунд. Программы, не укладывающиеся во время прохождения теста в установленные ограничения или выдающие ошибку, считаются не прошедшими данный тест.
1. Сверхнечетное число
Назовем натуральное число сверхнечетным, если оно состоит только из нечетных цифр. Требуется для заданного значения n найти n-е по счету сверхнечетное число.
Вход: файл input.txt, содержащий только натуральное число n.
Ограничения: 1 ≤ n ≤ 1000000.
Выход: файл output.txt, содержащий одно натуральное число – n-е по счету сверхнечетное число.
Пример:
| input.txt | output.txt |
| 13 | 35 |
2. Триангуляция
Задан многоугольник координатами своих вершин вдоль обхода его контура. Требуется указать множество непересекающихся во внутренних точках диагоналей, разбивающих многоугольник на треугольники.
Вход: файл input.txt, , в первой строке которого записано число N – количество вершин многоугольника, потом в N строках пары целых чисел – координат вершин многоугольника в порядке обхода контура.
Ограничения: 4 ≤ N ≤ 200; каждая координата от -10000 до 10000.
Выход: файл output.txt, в первой строке которого должно быть число k, указывающее необходимое число диагоналей. В последующих k строках должно быть по два натуральных числа – номер начальной и конечной вершины соответствующей диагонали.
Дополнительные ограничения: диагонали должны лежать строго внутри многоугольника (все точки диагонали, за исключением концов, являются внутренними точками многоугольника).
Пример:
| input.txt | output.txt |
|
5 1 1 2 5 5 5 5 1 2 2 |
2 2 5 3 5 |
3. Числовая прямая
На числовой прямой будем рассматривать только точки с целой координатой (в дальнейшем будем называть их целыми точками). Рассмотрим некоторое количество числовых промежутков, начало и конец которых являются целыми точками (предполагается, что начало и конец промежутка также входят в промежуток). С множествами чисел разрешается выполнять операции объединения, пересечения и разности:
Множество точек A+B содержит целые точки, которые принадлежат множеству A или множеству B (операция объединения).
Множество точек A*B содержит целые точки, которые принадлежат одновременно и множеству A, и множеству B (операция пересечения).
Множество точек A-B содержит целые точки, которые принадлежат множеству A, но не принадлежат множеству B (операция разности множеств).
Задано выражение, содержащее перечисленные операции. В выражении сначала выполняются операции пересечения, после этого операции сложения и вычитания (при этом операции сложения и вычитания имеют одинаковый приоритет). Для изменения порядка выполнения действий можно использовать круглые скобки.
Требуется определить множество точек (набор непересекающихся промежутков), являющееся значением заданного выражения для данных промежутков.
Вход: файл input.txt, содержащий несколько строк с описанием промежутков в следующем формате:
имя начало конец
После описания промежутков (не более 26) в последней строке файла input.txt следует выражение, содержащие имена промежутков (только из описанного выше набора), знаки операций над промежутками (+, – и *) и круглые скобки. Прочих символов (в том числе пробелов и других разделителей) выражение не содержит.
Ограничения:в описании каждого отрезка: имя – заглавная буква латинского алфавита (имя промежутка), начало и конец – целые числа от -2000000000 до 2000000000 (соответственно, начало и конец промежутка); длина выражения не превосходит 250.
Выход: файл output.txt, содержащий одну или несколько строк – перечисление непересекающихся промежутков, из которых состоит результирующее множество точек (результат применения заданного выражения к предложенному набору промежутков). В каждой строке приводится два целых числа – начало и конец промежутка, разделенные пробелом. Промежутки перечисляются в порядке расположения на числовой прямой слева направо (то есть в порядке возрастания координат левых концов).
Дополнительные ограничения: расстояние между соседними промежутками в выходном файле (разность между правым концом одного промежутка и левым концом другого) должно быть строго больше 1. Иначе говоря, смежные промежутки (те, между которыми нет целых точек) «сливаются» в один.
Пример 1:
| input.txt | output.txt |
|
A 1 5 B 3 7 A-B |
1 2 |
Пример 2:
| input.txt | output.txt |
|
D -5 10 K -4 5 R -7 2 D-K*R |
-5 -5 3 10 |
Пример 3:
| input.txt | output.txt |
|
W -10 -5 X 0 10 Y -7 5 Z 7 12 (W+X)*(Y+Z) |
-7 -5 0 5 7 10 |