Задания олимпиады по информатике – 2015

Решения задач загружаются в Виртуальном кабинете. Загрузка решений задач будет доступна со 2 ноября 2015 года.

Виртуальный кабинет

Каждая команда или индивидуальный участник получает после регистрации доступ к Виртуальному кабинету.
С помощью Виртуального кабинета команда/индивидуальный участник:

• публикует свою Визитную карточку
• узнает новости проекта, уточняет ключевые даты
• подает ответы на задания Интернет-олимпиады
• отправляет письма координатору
• оставить свои отзывы и пожелания организаторам проекта

 

Ключевые даты

Этапы выполнения заданий 1 тура	Дата получения (начала выполнения) задания	Дата окончания выполнения задания
Подготовка Визитки команды и загрузка файла через Виртуальный кабинет	после подтверждения регистрации	14-00 (мск) 1 ноября 2015 г.
Выполнение заданий проекта, загрузка работ через Виртуальный кабинет	11-00 (мск) 2 ноября 2015 г.	17-00 (мск) 11 ноября 2015 г.
Публикация итогов проекта		25 ноября 2015 г.
Команды отправляют отзыв о проекте из Виртуального кабинета.	До 28 ноября 2015 г.

Жюри имеет право дисквалифицировать участников олимпиады или аннулировать им баллы по отдельным задачам в следующих случаях:

• Использование участником олимпиады нескольких логинов, использование чужого логина.
• Отправка кода, пытающегося нарушить работу тестирующей системы.
• Публикация и обмен решениями задач в интернете.
• Сдача чужого решения, даже в том случае, если чужое решение было изменено или доработано.
• Передача своего решения другим участникам, даже непреднамеренная.

Задачи теоретической части

В предложенных задачах требуется дать словесное описание алгоритма решения предложенной задачи (если не оговаривается что-то другое). При проверке решений (алгоритмов) будут учитываться следующие параметры:

1. четкость описания алгоритма,
2. результативность (алгоритм в любом случае должен давать некоторый результат),
3. корректность (алгоритм должен давать правильный ответ при любых корректных входных данных),
4. оптимальность (следует привести по возможности наиболее оптимальный по количеству шагов алгоритм; из нескольких корректных алгоритмов больше баллов получит наиболее оптимальный).

Решения задач теоретической части оформляются в виде документа Microsoft Word в соответствии с техническими требованиями и загружаются для проверки в Виртуальном кабинете.

Задача 1. Цифры

Даны N цифр. Опишите эффективный алгоритм, который позволит составить из них 2 числа таким образом, чтобы их сумма была минимально возможной. Числа не должны иметь ведущих нулей.

Задача 2. Строки

Даны N строк s₁, s₂, …, s_n. Опишите эффективный алгоритм, позволяющий упорядочить их таким образом, чтобы конкатенация (склеивание) строк слева направо было минимальным в лексикографическом порядке.

Задача 3. Раскрасьте числа

Даны числа от 1 до N. Опишите эффективный алгоритм, раскрашивающий числа таким образом, чтобы если число A делится на число B, то числа A и B были окрашены в разный цвет. Число цветов должно быть минимально возможным.

Задача 4. Степени двойки

Все числа в массиве являются неотрицательными степенями двойки, не превосходящими 2015. Опишите алгоритм нахождения десяти подряд идущих элементов массива, среди которых нет одинаковых.

Задача 5. Стеклянные шары

Представьте, что вы находитесь в M-этажном здании. У вас есть B стеклянных шаров. Вам нужно найти самый высокий этаж, сбросив с которого шар, вы не сможете его разбить. Опишите эффективный алгоритм, позволяющий найти минимальное число бросков в худшем случае. Пример: если M=10, B=2, то минимальное число бросков – 4.

Задачи практической части

В практической части олимпиады требуется написать решения задач – программы, соответствующие техническим требованиям и выполняющие оговоренные условиями задачи действия, на языке Паскаль или Си.

Для проверки принимаются только исходные тексты программ (файлы *.pas, *.c, *.cpp) в соответствии с техническими требованиями. Программы (исходные тексты) загружаются для проверки в Виртуальном кабинете, сразу компилируются и проверяются на наборе тестов, после чего участнику выдается результат. Допускается вносить изменения в программы произвольное количество раз и загружать программы для повторной проверки.

Внимание: загрузка работ будет возможна со 2 ноября (c 11:00 МСК). Загружается только исходный текст программы (файл *.pas, *.c, *.cpp) без архивирования.

С учетом того, что проверка работ практической части ведется в автоматическом режиме, следует внимательно следить за форматами выходных файлов: несоответствие формата выходного файла может привести к тому, что результат прохождения теста не будет засчитан.

Входные данные берутся из текстового файла input.txt, результат выполнения программы выводится в файл output.txt в установленном формате. Программа ничего не должна запрашивать для ввода с клавиатуры и не должна ничего выводить на экран.

Ограничения на время выполнения программы по каждому из тестов: 2 секунды. Программы, не укладывающиеся во время прохождения теста в установленные ограничения или выдающие ошибку, считаются не прошедшими данный тест.

Задача 1. Видимые точки

Георгий так любит математику, что видит её практически во всём. Вот и отдыхая на пляже, он взял (N+1)x(N+1) камушков и разложил их в целочисленных точках квадрата размером NxN, находящегося в первой четверти плоскости. Левый нижний угол квадрата находится в точке (0,0), правый верхний – в точке (N,N).  Камушек, находящийся в точке (x,y) будем называть видимым, если на прямой, проведенной из (0,0) в (x,y), не лежит ни один другой камушек. Камушек, лежащий в точке (0,0), не считается видимым. Георгий хочет найти количество видимых камушков. Помогите ему это сделать. 

Вход: файл input.txt, в первой строке записано натуральное число N.

Ограничения: 1≤N≤10⁵

Выход: файл output.txt, содержащий единственное число – количество видимых камушков.

Примеры:

input.txt	output.txt
2	5
4	13
5	21

Примечание:

Ниже проиллюстрирован пример с видимыми точками в квадрате 5x5:

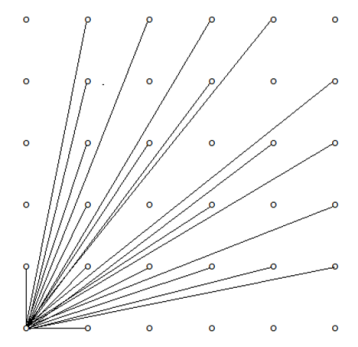
Задача 2. Необычное развлечение

Когда Георгию становится скучно на уроках математики, он развлекает себя следующим образом: берет натуральное число n и получает из него единицу с помощью последовательных  делений без остатка. На каждом шагу Георгий делит текущее число на любой его натуральный делитель, отличный от единицы.

Например, если n=30, то существует несколько способов получить из него единицу. Например, 30→10→1 или 30→6→3→1, или 30→1. Всего это можно сделать 13 способами.

Георгий просит вас помочь подсчитать количество способов, которыми он может получить из числа n единицу. Два способа n→x₁→…→x_k→1 и n→y₁→…→y_m→1 считаются различными, если k≠m или существует i такое, что x_i≠y_i.

Вход: файл input.txt, в первой строке записано натуральное число n.

Ограничения: 1≤N≤2*10⁹

Выход: файл output.txt, содержащий единственное число – количество способов получить из числа n единицу по модулю (10⁹+7) (т. е. вывести остаток от деления количества способов получить единицу на 10⁹+7).

Примеры:

input.txt	output.txt
1	1
9	2
30	13

Задача 3. Конструктор

Помимо математики Георгий любит собирать замки из конструкторов. В магазин завезли n конструкторов. Конструкторы пронумерованы числами от 1 до n.

У Георгия есть 2 способа получить нравящийся конструктор:

1. Купить его. Конструктор с номером i стоит c_i рублей;
2. Купить и объединить два конструктора, получив из них другой конструктор. Возможные способы компоновки конструкторов заданы тройками чисел (x, y, z). Купив конструкторы с номерами y и z, можно их объединить и получить один конструктор с номером x. Всего есть m доступных троек (x, y, z)

Георгий ограничен в средствах и просит вас помочь ему найти минимальную сумму денег, которую нужно будет потратить, чтобы собрать конструктор, из которого можно будет построить замок номер 1.

Вход: файл input.txt, в первой строке записаны два целых числа n и m. Во второй строке содержатся n чисел c_i  – стоимости конструкторов. В следующих m строках содержится по 3 числа x_i, y_i, z_i – это означает, что конструктор номер x_i может быть скомпонован из конструкторов y_i и z_i.  

Ограничения: 1≤ n≤ 10⁴, 0≤ m≤ 10⁵, 0 ≤ c_i ≤ 10⁹, 1 ≤x_i,y_i,z_i≤ n

Выход: файл output.txt, содержащий единственное число – минимальная сумма денег, которую потратит Георгий.

Примеры:

input.txt	output.txt
4 2 8 1 1 3 4 2 3 1 2 4	3
4 2 2 1 1 3 4 2 3 1 2 4	2

 

Примечание:

В первом тестовом примере, можно купить конструкторы номер 2 и 3, собрать из них детали для конструктора номер 4, затем купить ещё один конструктор номер 2 и собрать из имеющихся конструкторов конструктор номер 1. На это будет затрачено 1+1+1=3 рубля.