Задания для возрастной категории "7-8 классы"
Решения задач загружаются в Кабинете участника/команды. Загрузка решений задач будет доступна с 12:00 (мск) 6 ноября 2020 года.
Кабинет участника/команды
Каждая команда или индивидуальный участник получает после регистрации доступ к Кабинету участника/команды.
С помощью Кабинета команда/индивидуальный участник:
- узнает новости проекта, уточняет ключевые даты
- получает доступ к дистанционным мастер-классам
- подает ответы на задания Интернет-олимпиады в соответствии с техническими требованиями
- отправляет письма координатору
- оставляет отзывы об участии
- получает (скачивает) электронные сертификаты участия
Ключевые даты
|
Этапы выполнения заданий |
Дата |
|---|---|
|
1. Открывается форма для загрузки решений в Кабинете участника/команды |
12-00 (мск) 6 ноября 2020 г. |
|
2. Загрузка выполненных работ через Кабинет участника/команды |
до 17-00 (мск) |
|
3. Итоговые рейтинги команд публикуются на сайте |
12-00 (мск) |
| 4. Электронные сертификаты публикуются в Кабинете участника/команды | 12-00 (мск) 2 декабря 2020 г. |
|
5. Команды и участники отправляют отзыв об участии из Кабинета участника/команды |
до 4 декабря 2020 г. |
Задания для возрастной категории "7-8 классы"
Задание 1
Петя, Вася и Толя хотят установить одинаковый пароль на свои компьютеры – десятизначное число. Они могут пересылать друг другу информацию по электронной почте. Посылать пароль в незашифрованном виде они не хотят, т.к. знают, что почта может просматриваться. Как поступить ребятам?
Задание 2
15 гномов подошли к подвесному мосту, способному выдержать не более двух гномов одновременно. По мосту можно идти только с фонарём. Поодиночке они переходят мост в одну сторону за разное время, соответственно за 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5 минут. Когда идут вдвоем, то движутся со скоростью более медленного. Фонарь только один. За какое наименьшее число минут они все смогут переправиться на другую сторону моста? Требуется указать схему переходов и общее время. Обоснование минимальности можно не проводить.
Задание 3
Проводится лотерея. Предлагаются три конверта, в которых находятся три суммы денег – X, 2X и 4X рублей. Никакие действия (измерительные и т. п.) совершать с конвертами нельзя. Можно выбрать один конверт, посчитать в нем деньги, после чего сделать выбор — оставить этот конверт или взять другой конверт (при этом первый конверт из игры выбывает). Посмотрев, что лежит в нём, разрешается вместо него взять третий конверт, чтобы получить большую сумму. Ваши действия?
Задание 4
Даны две таблицы:
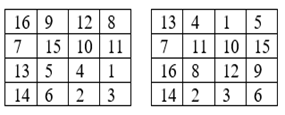
За один ход разрешается переставить в первой таблице два столбца или две строки. Можно ли за несколько ходов получить из первой таблицы вторую? Если нельзя, то разрешается перед началом ходов за 1 рубль поменять местами в первой таблице два числа. Если и в этом случае получить вторую таблицу не удастся, то ещё за 1 рубль можно поменять ещё два числа, и т.д. За какую наименьшую сумму можно решить задачу?
Задание 5
Для каждой из нижеперечисленных шахматных фигур найдите наименьшее количество цветов, в которые надо раскрасить клетки шахматной доски, чтобы никакие две фигуры, поставленные на клетки одинакового цвета, не угрожали друг другу.
А) конь, Б) слон, В) король, Г) ладья.
Задание 6
В энциклопедии выдающихся учёных указаны в алфавитном порядке фамилии живших ранее учёных. После каждой фамилии указаны годы жизни этого учёного, например,
Гаусс 1777 1885
Нейман 1903 1957
Пифагор -570 -490 (Отрицательные числа означают даты до нашей эры.)
Требуется описать алгоритм, определяющий год, в котором жило наибольшее число выдающихся учёных.