Задания для возрастной категории "5-6 классы"
Решения задач загружаются в Кабинете участника/команды. Загрузка решений задач будет доступна с 12:00 (мск) 6 ноября 2020 года.
Кабинет участника/команды
Каждая команда или индивидуальный участник получает после регистрации доступ к Кабинету участника/команды.
С помощью Кабинета команда/индивидуальный участник:
- узнает новости проекта, уточняет ключевые даты
- получает доступ к дистанционным мастер-классам
- подает ответы на задания Интернет-олимпиады в соответствии с техническими требованиями
- отправляет письма координатору
- оставляет отзывы об участии
- получает (скачивает) электронные сертификаты участия
Ключевые даты
|
Этапы выполнения заданий |
Дата |
|---|---|
|
1. Открывается форма для загрузки решений в Кабинете участника/команды |
12-00 (мск) 6 ноября 2020 г. |
|
2. Загрузка выполненных работ через Кабинет участника/команды |
до 17-00 (мск) |
|
3. Итоговые рейтинги команд публикуются на сайте |
12-00 (мск) |
| 4. Электронные сертификаты публикуются в Кабинете участника/команды | 12-00 (мск) 2 декабря 2020 г. |
|
5. Команды и участники отправляют отзыв об участии из Кабинета участника/команды |
до 4 декабря 2020 г. |
Задания для возрастной категории "5-6 классы"
Задание 1
Петя хочет переслать по электронной почте Васе секретный пароль X – десятизначное число. Посылать в незашифрованном виде он не хочет, т.к. знает, что почта может просматриваться. Как поступить ребятам?
Задание 2
Шесть гномов подошли к подвесному мосту, способному выдержать не более двух гномов одновременно. По мосту можно идти только с фонарём. Поодиночке гномы переходят мост в одну сторону за разное время, соответственно за 1, 2, 2, 4, 4, 4 минуты. Когда идут вдвоем, то движутся со скоростью более медленного. Фонарь только один. За какое наименьшее число минут они все смогут переправиться на другую сторону моста? Требуется указать схему переходов и общее время. Обоснование минимальности можно не приводить.
Задание 3
Проводится лотерея. Предлагаются два конверта, в которых находятся две суммы денег, причём в одном из конвертов сумма отличается от суммы в другом конверте ровно в два раза. Никакие действия (измерительные и т. п.) совершать с конвертами нельзя. Можно выбрать один конверт, посчитать в нем деньги, после чего сделать выбор — оставить этот конверт или взять другой конверт, желая получить большую сумму. Ваши действия?
Задание 4
Даны две таблицы:
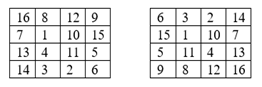
За один ход разрешается переставить в первой таблице два столбца или две строки. Можно ли за несколько ходов получить из первой таблицы вторую? Если да, то как, если нет, то почему.
Задание 5
На шахматной доске стоят несколько ладей. Докажите, что их можно раскрасить тремя цветами, чтобы одноцветные ладьи не стояли под боем друг друга. Хватит ли для этого двух цветов?
Задание 6
В теннисном турнире заявлено 16 участников. Известно, что в личной встрече всегда выигрывает более сильный игрок. Сколько надо сыграть игр, чтобы выделить
А) одного победителя;
Б) победителя и второго по силе игрока;
В) тройку призёров (первого, второго и третьего)
Пункты Б и В можно не обосновывать.